
Visual Hexadecimal
By Dinal Andreasen View In Digital Edition
When the digital age began, development proceeded rapidly and precedents were set that will probably never be reconsidered. Armed with a limited alpha-numeric keyboard and the concept of context and abstraction, digital pioneers adopted the hexadecimal system as the standard way to represent base 16 numbers. Sixteen unique symbols 0123456789ABCDEF represent each of the numerals from 0 to 15. The drawback of hexadecimal is it suffers from mixing the Arabic number system which has been vetted for thousands of years, with a rush to represent six additional numerals to create a 16 position radix.
There hasn’t been widespread acceptance of appropriate unique names for the numerals above 10. Eighty works well in the English language, but try telling someone A8 by saying “A”ty eight. It’s awkward and difficult to communicate verbally when a mixture of alphabetical and numerical symbols are used.
That’s not to say that all hex is difficult to verbalize. Hexspeak developed using common words made from only hexadecimal characters [https://en.wikipedia.org/wiki/Hexspeak]. The first one I remember using was C0FFEE which was used as a sync word in shared memory to indicate a processor had successfully booted and was ready to read and write from shared memory.
Check out Bibi-binary on Wikipedia [https://en.wikipedia.org/wiki/Bibi-binary] for a proposed alternative to hexadecimal notation which fortunately (or unfortunately depending on your opinion) has not received widespread acceptance. The Bibi-binary system devised by Lapointe includes unique symbols to use for all 16 numerals.
He also devised a very logical pronunciation for each of the numerals using four common consonants and four common vowels. For example, 7D0 is pronounced BiDaHo. Our example of A8 would be pronounced KeHo.
The purpose of this article is not to change the way hex is written or pronounced. The goal is to provide a visual memory association to minimize mental fumbling when dealing with hex notation.
When doing digital design, one must reluctantly accept that after nine, the letters A-F represent the next six numbers. This is probably easier for some digital designers who are naturally talented at abstraction, context, and recursion. For the rest of us, hard work and memory association techniques can ease the hexadecimal struggle.
The letters A through F represent a binary count starting after nine. Every hexadecimal number represented by the characters A through F has a bit 8 set. For memory association, bit 8 is represented by the front wheel of a car.
A is reasonably easy to remember (Figure 1).
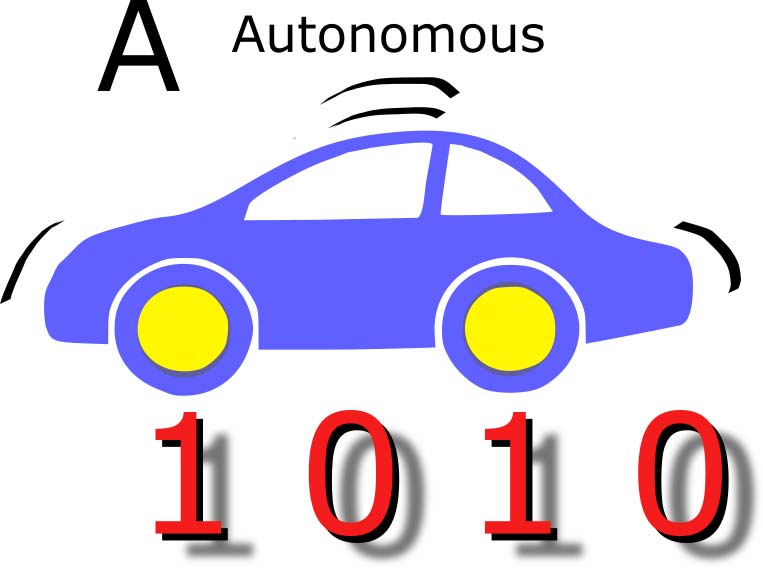
FIGURE 1. Hexadecimal A.
It represents a count of 10, and if you go through the mental steps of converting decimal to binary, you come up with an 8 and a 2 which is 1010. A also has the unique property that it complements 5 and provides an alternating pattern of ones and zeroes; 1010 where 5 is 0101. For A, think of an autonomous vehicle that is a short car without a driver between the wheels.
The challenging digits are B, C, and D (Figures 2-4).
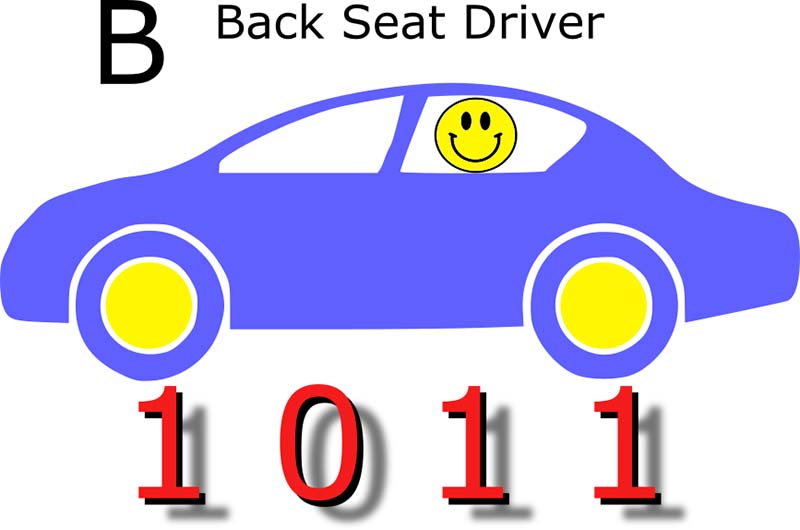
FIGURE 2. Hexadecimal B.

FIGURE 3. Hexadecimal C.
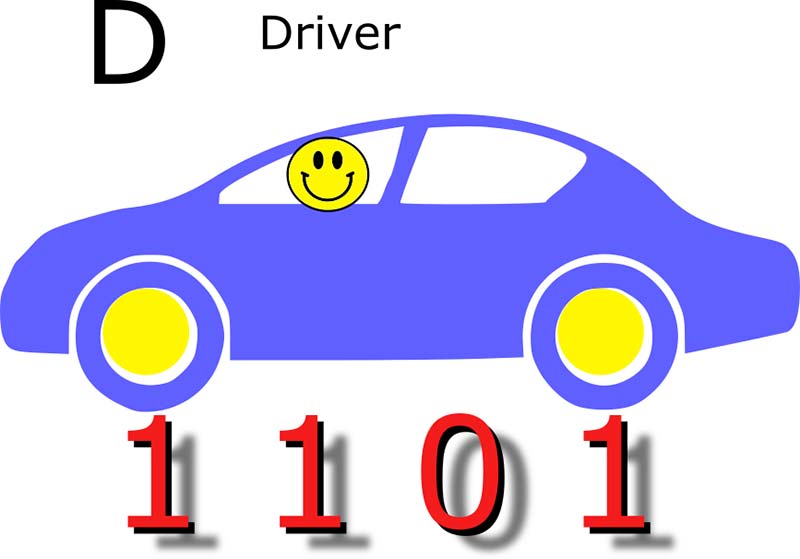
FIGURE 4. Hexadecimal D.
One can spend time with various methods to first convert to a count and then convert the count as a decimal number to binary. B is a count of 11 which after subtracting 8 leaves 3, meaning to set the 8 bit, the 2 bit, and the 1 bit.
Like Jethro in the Beverly Hillbillies used to say, “That’s way too much ciphering.”
A faster way is to associate B with a back seat driver. There is not a driver in the front seat, which represents the 0. The front tire is a 1, the back seat driver is a 1, and the rear tire is a 1.
For C, the memorization tool is to associate with a crashed car. The tires are right next to each other. There is no driver and there is no one in the backseat. C is a 12 which means the 8 bit is set and the 4 bit is set.
D is a driver. The driver is in the front seat. There is no one in the back seat. D is a count of 13 which has the 8, the 4, and the 1 bit set.
The hexadecimal number E (Figure 5) can be associated with an electric vehicle.
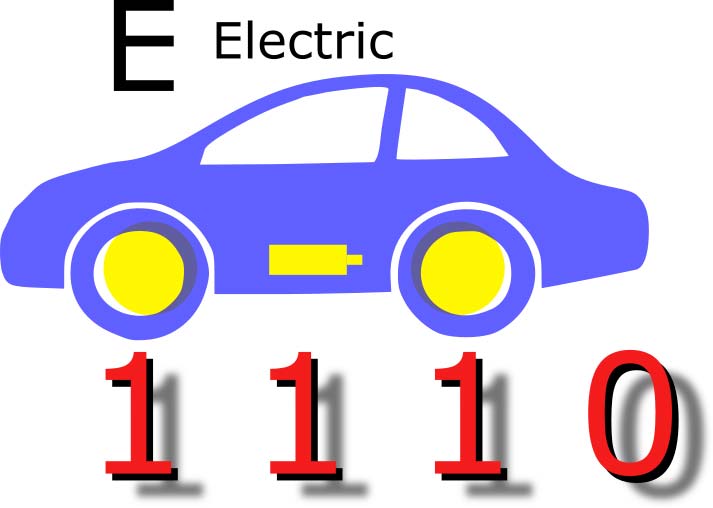
FIGURE 5. Hexadecimal E.
Think of a small vehicle with the compartment between the wheels under the floorboard containing the battery. The front tire is a 1, the battery is a 1, and the rear tire is a 1.
F is easy because it is all ones — the last binary count before rolling over — so it’s 1111 or 15 (Figure 6).

FIGURE 6. Hexadecimal F.
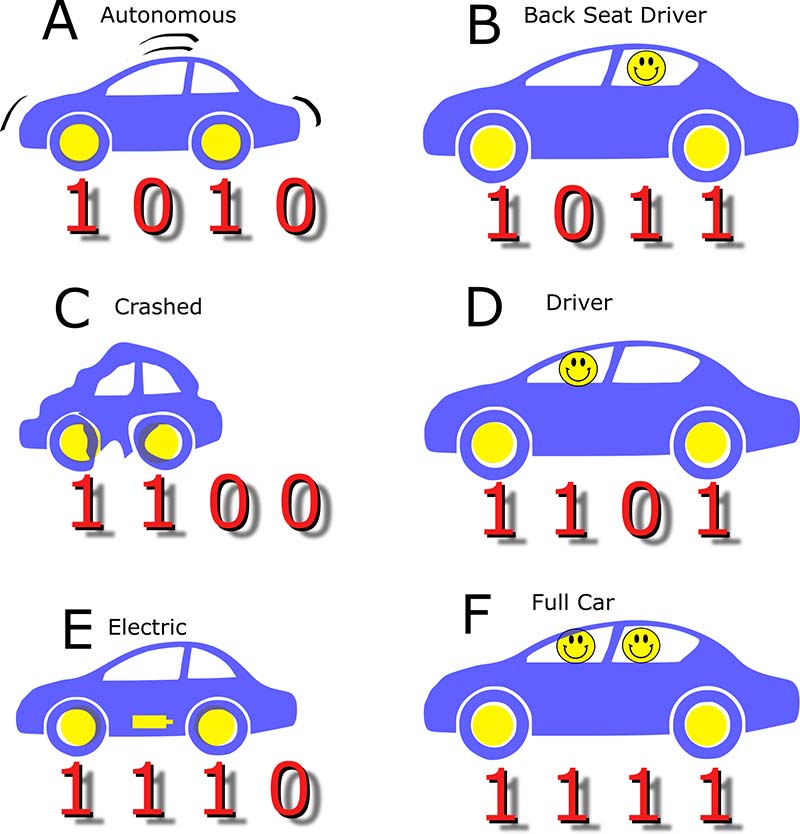
FIGURE 7. Hexadecimal A-F.
F is a full car. Two wheels on the ground and two happy passengers in the car. They are happy now that they can quickly go from hex to binary using the visual tools we just went over. SV
Article Comments